Hypothesis testing evaluates evidence against a null hypothesis to determine statistical significance, often relying on p-values to decide whether to reject it. Bayesian inference incorporates prior knowledge and observed data to update the probability of a hypothesis, providing a probabilistic interpretation of results. These approaches differ fundamentally in their treatment of uncertainty and decision-making in scientific research.
Table of Comparison
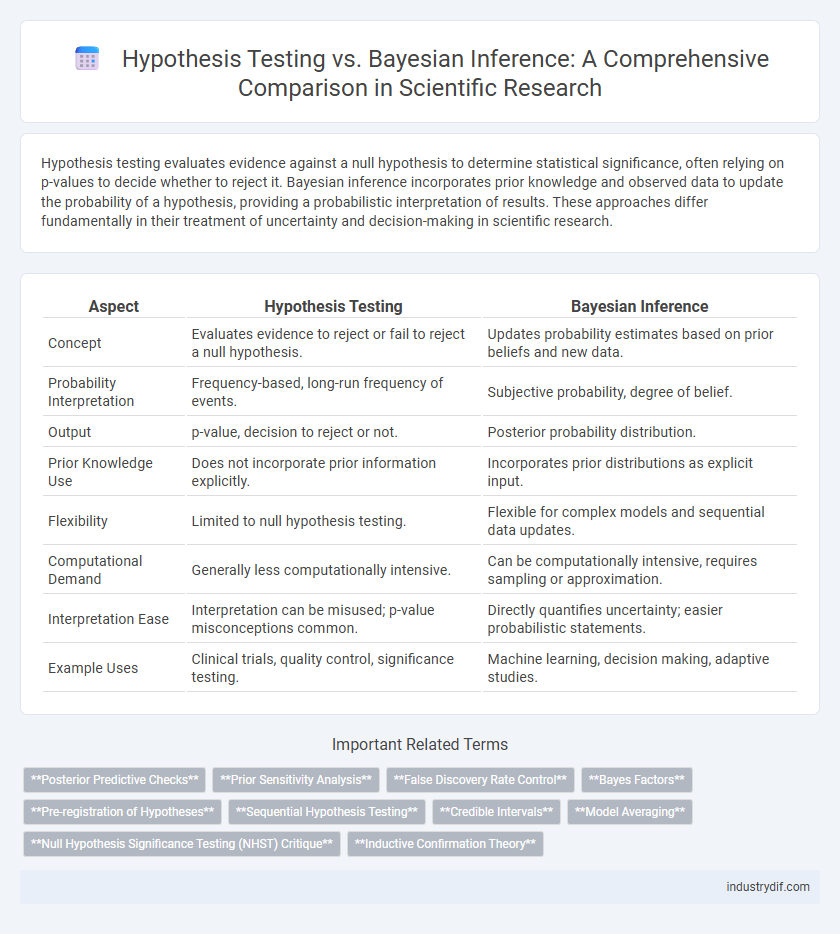
| Aspect | Hypothesis Testing | Bayesian Inference |
|---|---|---|
| Concept | Evaluates evidence to reject or fail to reject a null hypothesis. | Updates probability estimates based on prior beliefs and new data. |
| Probability Interpretation | Frequency-based, long-run frequency of events. | Subjective probability, degree of belief. |
| Output | p-value, decision to reject or not. | Posterior probability distribution. |
| Prior Knowledge Use | Does not incorporate prior information explicitly. | Incorporates prior distributions as explicit input. |
| Flexibility | Limited to null hypothesis testing. | Flexible for complex models and sequential data updates. |
| Computational Demand | Generally less computationally intensive. | Can be computationally intensive, requires sampling or approximation. |
| Interpretation Ease | Interpretation can be misused; p-value misconceptions common. | Directly quantifies uncertainty; easier probabilistic statements. |
| Example Uses | Clinical trials, quality control, significance testing. | Machine learning, decision making, adaptive studies. |
Fundamental Concepts: Hypothesis Testing and Bayesian Inference
Hypothesis testing evaluates data against a null hypothesis using p-values to determine statistical significance, emphasizing error rates and fixed thresholds. Bayesian inference incorporates prior knowledge with observed data to update probability estimates through Bayes' theorem, offering a probabilistic interpretation of hypotheses. These fundamental differences underscore distinct approaches to uncertainty and decision-making in scientific analysis.
Statistical Philosophies: Frequentist vs Bayesian Approaches
Frequentist hypothesis testing interprets probability as long-run frequencies, emphasizing null hypothesis significance testing and p-values to make inferences without incorporating prior information. Bayesian inference treats probability as a measure of belief, updating prior distributions with observed data to generate posterior probabilities that directly quantify uncertainty about parameters. These contrasting statistical philosophies influence approach to data analysis, with Frequentist methods relying on fixed parameters and repeated sampling, while Bayesian models integrate prior knowledge for more flexible, interpretable conclusions.
Formulation of Hypotheses in Scientific Research
Formulation of hypotheses in scientific research under hypothesis testing involves stating a null hypothesis (H0) and an alternative hypothesis (H1), which are then subjected to statistical tests for rejection or acceptance based on p-values. Bayesian inference formulates hypotheses by integrating prior distributions representing existing knowledge with observed data to compute posterior probabilities, enabling a continuous update of belief about the hypotheses. This contrast highlights that hypothesis testing relies on fixed hypotheses and frequency-based decision rules, while Bayesian inference treats hypotheses probabilistically and updates their credibility as evidence accumulates.
Probability Interpretations: Objective vs Subjective Views
Hypothesis testing relies on the frequentist interpretation of probability, treating it as the long-run frequency of events, which provides an objective framework for decision-making in scientific experiments. Bayesian inference interprets probability subjectively, representing an individual's degree of belief based on prior knowledge and evidence, allowing for dynamic updating of uncertainties. This fundamental difference in probability interpretation shapes the methodologies and conclusions drawn from data analysis in research contexts.
p-Values and Statistical Significance Explained
P-values quantify the probability of observing data as extreme as the sample given that the null hypothesis is true, guiding decisions about statistical significance in hypothesis testing. Statistical significance is commonly determined by comparing the p-value to a predefined alpha level, often 0.05, to reject or fail to reject the null hypothesis. In contrast, Bayesian inference updates prior beliefs with observed data to produce a posterior distribution, providing a probabilistic framework that explicitly incorporates uncertainty rather than relying solely on p-value thresholds.
Bayesian Credible Intervals vs Confidence Intervals
Bayesian credible intervals represent the probability that a parameter lies within a specific range given the observed data and prior information, providing a direct probabilistic interpretation. Confidence intervals, derived from frequentist hypothesis testing, indicate a range that would contain the true parameter in a specified percentage of repeated samples, lacking direct probability statements about the parameter itself. The fundamental distinction lies in Bayesian credible intervals incorporating prior distributions for parameter estimation, whereas confidence intervals rely solely on the sampling distribution of the estimator.
Model Updating: Learning from Data in Both Frameworks
Hypothesis testing relies on fixed models with predefined null and alternative hypotheses, evaluating data by calculating p-values to accept or reject hypotheses without inherently updating beliefs. Bayesian inference continuously updates model parameters and uncertainty through posterior distributions based on prior knowledge combined with new data, enabling dynamic learning from evidence. This iterative model updating in Bayesian framework provides a flexible and coherent approach to learning from data compared to the static nature of traditional hypothesis testing.
Use Cases: When to Apply Hypothesis Testing or Bayesian Inference
Hypothesis testing is ideal for scenarios requiring a clear decision based on fixed significance levels, such as clinical trials assessing treatment efficacy or quality control in manufacturing processes. Bayesian inference excels in complex models involving prior knowledge integration and continuous learning, often used in machine learning algorithms and adaptive decision-making systems. Selecting between these methods depends on the availability of prior data, the need for probabilistic interpretation, and the specific objectives of the analysis.
Advantages and Limitations in Scientific Applications
Hypothesis testing offers a straightforward framework for decision-making through p-values and significance levels, facilitating clear-cut conclusions in controlled experimental settings. Bayesian inference incorporates prior knowledge and updates probabilities with new data, providing a flexible and intuitive approach for complex models and sequential analysis. However, hypothesis testing may oversimplify uncertainty and is sensitive to sample size, while Bayesian methods can be computationally intensive and reliant on subjective prior distributions, posing challenges in scientific reproducibility.
Future Trends in Statistical Inference Methods
Emerging trends in statistical inference highlight a shift toward integrating Bayesian inference with traditional hypothesis testing to enhance decision-making under uncertainty. Advances in computational power facilitate the application of complex Bayesian hierarchical models, enabling more nuanced interpretations of data in fields such as genomics and climate science. Future methodologies are expected to leverage machine learning algorithms alongside Bayesian frameworks to improve predictive accuracy and real-time data assimilation.
Related Important Terms
Posterior Predictive Checks
Posterior predictive checks utilize Bayesian inference to generate replicated data sets from the posterior distribution, enabling assessment of model fit by comparing observed data to predictive simulations. Unlike traditional hypothesis testing, which relies on p-values to reject null hypotheses, posterior predictive checks provide a probabilistic framework to identify model discrepancies through graphical or quantitative summaries.
Prior Sensitivity Analysis
Prior sensitivity analysis in hypothesis testing evaluates how variations in prior assumptions influence posterior probabilities, ensuring robustness in Bayesian inference conclusions. This process identifies the impact of different prior distributions on parameter estimates, crucial for validating model reliability in scientific research.
False Discovery Rate Control
False Discovery Rate (FDR) control in hypothesis testing relies on p-value adjustments, such as the Benjamini-Hochberg procedure, to limit the expected proportion of type I errors among rejected hypotheses. Bayesian inference, by contrast, addresses FDR through posterior probabilities and decision-theoretic frameworks, providing more flexible control over false discoveries by incorporating prior information and updating beliefs with observed data.
Bayes Factors
Bayes Factors quantify evidence in favor of one statistical model over another by comparing their marginal likelihoods, providing a continuous measure of support that contrasts with the binary decision framework of traditional hypothesis testing. Unlike p-values, Bayes Factors allow researchers to update the strength of evidence with accumulating data, enabling more nuanced conclusions in Bayesian inference.
Pre-registration of Hypotheses
Pre-registration of hypotheses enhances the rigor of hypothesis testing by specifying analysis plans before data collection, reducing bias and p-hacking. Bayesian inference benefits from pre-registration through transparent prior selection and model specifications, improving reproducibility and interpretability of posterior results.
Sequential Hypothesis Testing
Sequential hypothesis testing dynamically evaluates data as it is collected, allowing for decisions to be made at any stage without fixed sample sizes, thereby optimizing resource allocation and reducing experimental costs. Bayesian inference incorporates prior knowledge and continuously updates posterior probabilities with new evidence, enhancing flexibility and interpretability in sequential analysis frameworks.
Credible Intervals
Credible intervals in Bayesian inference provide a probabilistic range within which parameters lie with a specified probability, reflecting direct uncertainty about the parameter. In contrast, confidence intervals from hypothesis testing offer long-run frequency properties without assigning probability to the parameter itself.
Model Averaging
Model averaging in hypothesis testing integrates multiple candidate models to account for model uncertainty, enhancing predictive accuracy by weighting models based on their fit and complexity. Bayesian inference inherently supports model averaging through posterior model probabilities, allowing probabilistic combination of models and facilitating more robust decision-making under uncertainty.
Null Hypothesis Significance Testing (NHST) Critique
Null Hypothesis Significance Testing (NHST) faces criticism for its binary outcome that oversimplifies evidence by focusing solely on p-values without quantifying the strength of hypotheses, often leading to misinterpretation and replication issues in scientific research. Bayesian inference offers a robust alternative by integrating prior knowledge and providing probability distributions over parameters, thus enhancing decision-making and inferential clarity beyond the limitations of NHST.
Inductive Confirmation Theory
Inductive confirmation theory evaluates hypotheses by measuring how evidence increases the probability of a hypothesis, aligning more closely with Bayesian inference, which updates beliefs through prior and posterior probabilities. Hypothesis testing, by contrast, relies on rejecting or failing to reject null hypotheses without providing probabilistic confirmation, limiting its capacity to confirm hypotheses inductively.
Hypothesis Testing vs Bayesian Inference Infographic
 industrydif.com
industrydif.com