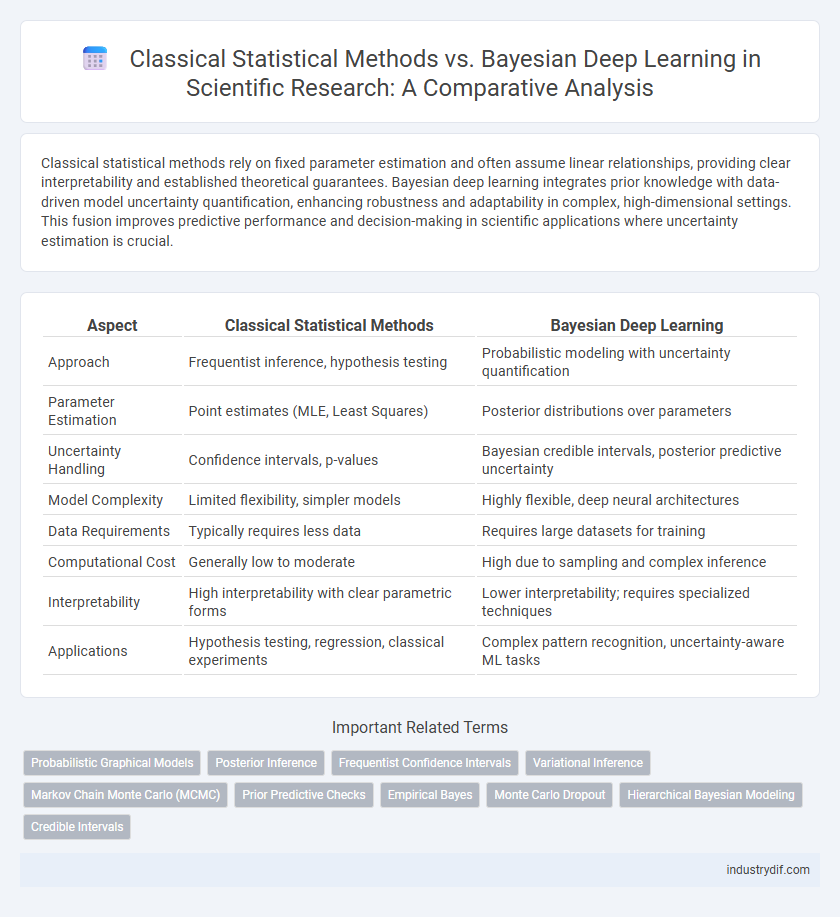
Classical statistical methods rely on fixed parameter estimation and often assume linear relationships, providing clear interpretability and established theoretical guarantees. Bayesian deep learning integrates prior knowledge with data-driven model uncertainty quantification, enhancing robustness and adaptability in complex, high-dimensional settings. This fusion improves predictive performance and decision-making in scientific applications where uncertainty estimation is crucial.
Table of Comparison
| Aspect | Classical Statistical Methods | Bayesian Deep Learning |
|---|---|---|
| Approach | Frequentist inference, hypothesis testing | Probabilistic modeling with uncertainty quantification |
| Parameter Estimation | Point estimates (MLE, Least Squares) | Posterior distributions over parameters |
| Uncertainty Handling | Confidence intervals, p-values | Bayesian credible intervals, posterior predictive uncertainty |
| Model Complexity | Limited flexibility, simpler models | Highly flexible, deep neural architectures |
| Data Requirements | Typically requires less data | Requires large datasets for training |
| Computational Cost | Generally low to moderate | High due to sampling and complex inference |
| Interpretability | High interpretability with clear parametric forms | Lower interpretability; requires specialized techniques |
| Applications | Hypothesis testing, regression, classical experiments | Complex pattern recognition, uncertainty-aware ML tasks |
Introduction to Classical Statistical Methods
Classical statistical methods rely on well-defined probability models and inference techniques such as hypothesis testing, maximum likelihood estimation, and linear regression to analyze data. These methods assume fixed parameters and use sample data to make point estimates and confidence intervals based on frequentist principles. Their interpretability and computational efficiency make them foundational tools for traditional data analysis and hypothesis-driven research.
Fundamentals of Bayesian Deep Learning
Bayesian Deep Learning integrates probability theory with neural networks to quantify uncertainty in model predictions, enhancing robustness in decision-making processes. Unlike classical statistical methods that rely on point estimates and fixed parameter assumptions, Bayesian approaches treat model parameters as probability distributions, allowing for continuous updating of beliefs with incoming data. This fundamental shift enables better handling of model uncertainty, improved generalization, and more reliable inference in complex, high-dimensional scenarios.
Key Differences: Classical vs Bayesian Approaches
Classical statistical methods rely on fixed parameters and frequentist inference, emphasizing point estimates and hypothesis testing to draw conclusions from data. Bayesian deep learning incorporates probabilistic modeling with prior knowledge, updating beliefs through posterior distributions, enabling uncertainty quantification and more flexible inference. The key difference lies in Bayesian approaches treating model parameters as random variables, while classical methods treat them as fixed but unknown quantities.
Probabilistic Modeling in Scientific Research
Classical statistical methods rely on fixed parameter estimation and hypothesis testing, often assuming linearity and normality in data distributions. Bayesian deep learning incorporates probabilistic modeling by using prior distributions and posterior inference to quantify uncertainty in complex, high-dimensional scientific data. This approach enhances model interpretability and robustness, enabling more accurate predictions and decision-making under uncertainty in scientific research.
Interpretability and Uncertainty Quantification
Classical statistical methods provide transparent interpretability through well-defined models and clear inferential procedures, enabling straightforward uncertainty quantification via confidence intervals and p-values. Bayesian deep learning leverages probabilistic frameworks to capture model uncertainty and offer richer uncertainty quantification by integrating prior knowledge with data-driven posterior distributions. Despite Bayesian approaches improving uncertainty estimates, their interpretability remains challenging due to model complexity and the high-dimensional nature of deep neural networks.
Computational Complexity and Scalability
Classical statistical methods often rely on closed-form solutions or iterative algorithms with polynomial-time complexity, enabling efficient computation on moderate-sized datasets but struggling with scalability in high-dimensional or large-scale problems. Bayesian deep learning introduces probabilistic inference through neural networks, which typically requires extensive sampling methods like Markov Chain Monte Carlo or variational inference, significantly increasing computational complexity and training time. Despite higher complexity, Bayesian deep learning offers scalable model uncertainty estimation and adaptive capacity, making it suitable for large, complex datasets when optimized with hardware accelerators and approximate inference techniques.
Data Requirements and Prior Knowledge
Classical statistical methods typically require larger datasets to achieve reliable parameter estimation, relying on frequentist assumptions and limited incorporation of prior knowledge. Bayesian deep learning leverages prior distributions and probabilistic modeling, enabling effective learning from smaller datasets while quantifying uncertainty. This integration of prior knowledge and data-driven updates enhances model robustness in complex scientific domains with limited experimental data.
Applications in Scientific Experiments
Classical statistical methods provide robust frameworks for hypothesis testing and experimental design, emphasizing parameter estimation and confidence intervals in controlled scientific experiments. Bayesian deep learning enhances these approaches by incorporating uncertainty quantification and probabilistic modeling, enabling more adaptive and interpretable analysis in complex, high-dimensional data settings such as genomics and climate modeling. The integration of Bayesian inference with deep learning techniques facilitates more precise predictions and dynamic updates to models as new experimental data becomes available.
Limitations and Challenges of Each Method
Classical statistical methods often struggle with high-dimensional data and model assumptions that limit flexibility, such as normality and linearity, which can impair their effectiveness in complex scientific problems. Bayesian deep learning offers improved uncertainty quantification and adaptability through hierarchical priors but faces challenges in computational scalability and risk of model misspecification. Both approaches require careful consideration of data quality and computational resources to ensure robustness and interpretability in scientific applications.
Future Trends in Scientific Data Analysis
Emerging trends in scientific data analysis reveal a shift from classical statistical methods, such as regression and hypothesis testing, towards Bayesian deep learning frameworks that offer enhanced uncertainty quantification and model adaptability. Bayesian approaches integrate prior knowledge with observed data, improving predictive accuracy in complex, high-dimensional scientific datasets. Future research is likely to emphasize hybrid models combining interpretability of classical statistics with the computational power of deep learning for robust, scalable data analysis across disciplines.
Related Important Terms
Probabilistic Graphical Models
Probabilistic Graphical Models (PGMs) in classical statistical methods provide structured representations of conditional dependencies using fixed probabilistic frameworks, enabling interpretability and well-established inference algorithms. Bayesian Deep Learning integrates PGMs within neural networks to capture uncertainty in complex, high-dimensional data through posterior distributions, enhancing robustness and predictive performance in probabilistic reasoning tasks.
Posterior Inference
Classical statistical methods rely on closed-form solutions or asymptotic approximations for posterior inference, often limiting flexibility in complex models. Bayesian deep learning utilizes variational inference or Markov Chain Monte Carlo techniques to approximate posterior distributions, enabling scalable uncertainty quantification in high-dimensional parameter spaces.
Frequentist Confidence Intervals
Frequentist confidence intervals quantify the range within which a parameter lies based on repeated sampling and fixed true values, relying on classical statistical assumptions and large-sample approximations. In contrast, Bayesian deep learning integrates prior distributions and updates uncertainty through posterior distributions, offering a more flexible and data-driven approach to uncertainty quantification beyond frequentist confidence bounds.
Variational Inference
Variational inference in Bayesian deep learning offers a scalable alternative to classical statistical methods by approximating posterior distributions through optimization, enhancing model uncertainty quantification and flexibility. Unlike traditional frequentist approaches relying on point estimates, variational techniques enable efficient Bayesian inference in complex neural networks, improving predictive performance and interpretability.
Markov Chain Monte Carlo (MCMC)
Markov Chain Monte Carlo (MCMC) methods in Bayesian deep learning provide probabilistic inference by generating samples from complex posterior distributions, overcoming limitations of classical statistical methods that often rely on point estimates and asymptotic approximations. Unlike traditional techniques, MCMC enables uncertainty quantification and model flexibility, facilitating improved prediction accuracy and interpretability in high-dimensional parameter spaces.
Prior Predictive Checks
Prior predictive checks in classical statistical methods rely on fixed probability distributions to validate model assumptions before observing data, whereas Bayesian deep learning incorporates prior knowledge through hierarchical priors and probabilistic layering, enhancing model flexibility and uncertainty quantification. By leveraging Bayesian inference, prior predictive checks enable more robust assessment of model fit and predictive performance in complex, high-dimensional data contexts typical of deep learning applications.
Empirical Bayes
Empirical Bayes methods bridge Classical Statistical Methods and Bayesian Deep Learning by estimating prior distributions directly from the data, enhancing parameter inference in hierarchical models. This approach integrates frequentist consistency with Bayesian regularization, improving model adaptability and predictive performance in complex datasets.
Monte Carlo Dropout
Monte Carlo Dropout integrates classical statistical methods with Bayesian deep learning by approximating posterior distributions through stochastic forward passes, enabling uncertainty quantification in neural networks. This approach leverages dropout as a variational inference technique, providing scalable and computationally efficient uncertainty estimates compared to traditional frequentist statistics.
Hierarchical Bayesian Modeling
Hierarchical Bayesian Modeling enhances Bayesian deep learning by structuring complex data with multiple levels of uncertainty, surpassing classical statistical methods in capturing parameter variability across groups. This approach facilitates more accurate inference with limited data through prior distributions that share strength across hierarchical layers, improving model robustness and interpretability.
Credible Intervals
Classical statistical methods typically use confidence intervals based on frequentist probability to quantify uncertainty, whereas Bayesian deep learning employs credible intervals derived from posterior distributions, offering a probabilistic interpretation that directly reflects uncertainty about model parameters. Credible intervals in Bayesian frameworks provide more intuitive and informative measures of uncertainty, especially in complex models with hierarchical structures or limited data.
Classical Statistical Methods vs Bayesian Deep Learning Infographic
 industrydif.com
industrydif.com