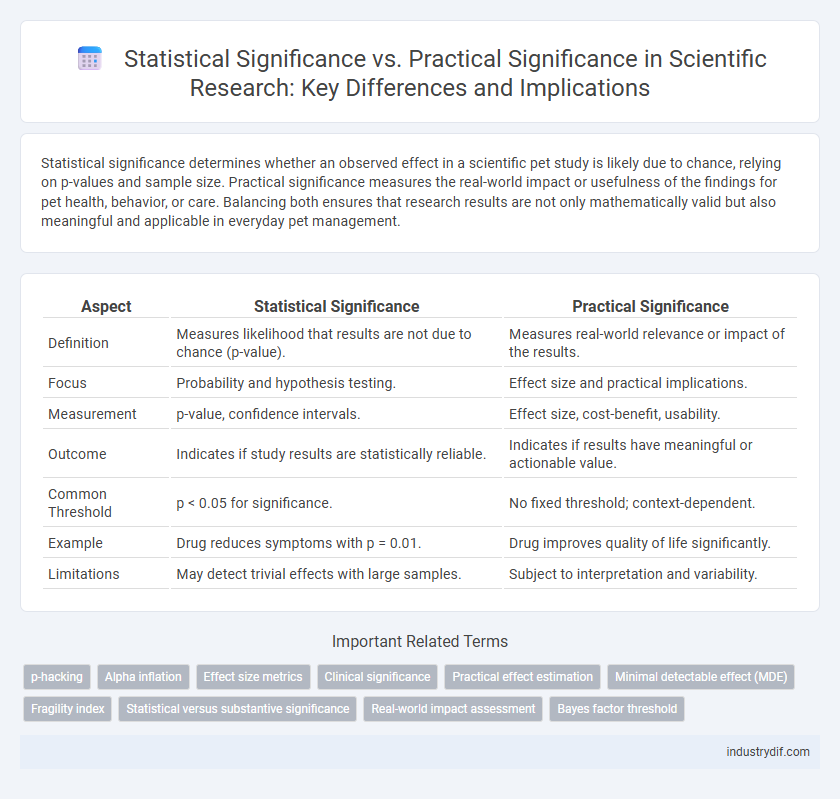
Statistical significance determines whether an observed effect in a scientific pet study is likely due to chance, relying on p-values and sample size. Practical significance measures the real-world impact or usefulness of the findings for pet health, behavior, or care. Balancing both ensures that research results are not only mathematically valid but also meaningful and applicable in everyday pet management.
Table of Comparison
| Aspect | Statistical Significance | Practical Significance |
|---|---|---|
| Definition | Measures likelihood that results are not due to chance (p-value). | Measures real-world relevance or impact of the results. |
| Focus | Probability and hypothesis testing. | Effect size and practical implications. |
| Measurement | p-value, confidence intervals. | Effect size, cost-benefit, usability. |
| Outcome | Indicates if study results are statistically reliable. | Indicates if results have meaningful or actionable value. |
| Common Threshold | p < 0.05 for significance. | No fixed threshold; context-dependent. |
| Example | Drug reduces symptoms with p = 0.01. | Drug improves quality of life significantly. |
| Limitations | May detect trivial effects with large samples. | Subject to interpretation and variability. |
Defining Statistical Significance
Statistical significance measures the likelihood that an observed effect or relationship in data is not due to random chance, typically assessed through p-values and confidence intervals. A result is deemed statistically significant when the p-value falls below a predetermined threshold, often 0.05, indicating strong evidence against the null hypothesis. This concept is essential in hypothesis testing within scientific research to determine whether findings are reliable and warrant further consideration.
Understanding Practical Significance
Practical significance measures the real-world relevance or impact of a study's findings beyond mere statistical significance, which only indicates the likelihood that results are not due to chance. Effect size and confidence intervals play a crucial role in assessing practical significance by quantifying the magnitude and reliability of an observed effect. Researchers must consider the context, cost-benefit analysis, and applicability to ensure findings translate into meaningful outcomes in scientific practice.
Key Differences Between Statistical and Practical Significance
Statistical significance measures whether an observed effect is likely due to chance using p-values and confidence intervals, while practical significance evaluates the real-world relevance or impact of that effect. Key differences include statistical significance relying heavily on sample size and hypothesis testing, whereas practical significance considers the magnitude and applicability of the results in a specific context. Understanding these distinctions is crucial in scientific research to avoid misinterpreting findings that are statistically significant but lack meaningful practical implications.
Common Misconceptions in Data Interpretation
Statistical significance often gets misinterpreted as practical importance, leading to incorrect conclusions in data analysis. A p-value merely indicates the likelihood of observing the data if the null hypothesis is true, but it does not measure the effect size or its real-world impact. Ignoring effect size and confidence intervals contributes to the misconception that statistically significant results always imply meaningful or actionable findings.
The Role of Sample Size in Statistical Significance
Sample size plays a crucial role in determining statistical significance, as larger samples tend to produce smaller p-values, increasing the likelihood of detecting even trivial effects. However, statistical significance achieved with large samples does not necessarily imply practical significance, as the observed effect size might be too small to matter in real-world applications. Researchers must interpret results by considering both sample size and effect magnitude to make meaningful conclusions about the relevance of their findings.
Effect Size: A Bridge Between Theory and Practice
Effect size quantifies the magnitude of a relationship or difference, providing crucial context beyond p-values in statistical significance. It bridges theory and practice by conveying the practical impact of findings in real-world settings, allowing researchers to assess the relevance and importance of results. Understanding effect size enhances decision-making by highlighting the substantive, not just statistical, significance of scientific outcomes.
Real-World Implications of Practical Significance
Practical significance assesses the real-world impact of research findings beyond mere statistical results, emphasizing the magnitude and relevance of effects in applied settings. While statistical significance indicates the likelihood that an observed effect is not due to chance, practical significance evaluates whether the effect size is substantial enough to influence decisions or policies. This distinction is crucial in fields such as medicine and social sciences, where statistically significant results may have negligible practical benefits or implications for patient outcomes and societal advancements.
Reporting Results: Best Practices for Scientists
When reporting results, scientists must distinguish between statistical significance, which indicates the likelihood that the observed effect is not due to chance, and practical significance, which reflects the real-world relevance or magnitude of the effect. Clear presentation of effect sizes, confidence intervals, and context-specific implications enhances transparency and aids in interpreting the scientific importance beyond p-values. Including both statistical and practical significance in research reports ensures findings are communicated accurately for informed decision-making and future research directions.
Case Studies Illustrating Both Concepts
Case studies in clinical trials often reveal statistical significance through p-values below 0.05, while practical significance is measured by the actual improvement in patient outcomes. For instance, a large sample size may detect a statistically significant but clinically negligible reduction in blood pressure. Conversely, a smaller pilot study might show a meaningful effect size that impacts treatment decisions despite lacking statistical significance.
Guidelines for Balancing Statistical and Practical Significance in Research
Balancing statistical significance and practical significance requires researchers to interpret p-values alongside effect sizes and confidence intervals to assess real-world impact. Applying domain-specific thresholds and considering cost-benefit analyses ensures that findings are both statistically valid and meaningful for decision-making. Incorporating stakeholder perspectives further refines the relevance and applicability of research outcomes.
Related Important Terms
p-hacking
Statistical significance relies on p-values to determine if results are likely due to chance, but p-hacking manipulates data or analyses to achieve artificially low p-values, compromising the integrity of findings. Practical significance evaluates the real-world impact or effect size of results, highlighting that statistically significant outcomes may lack meaningful or applicable value despite their low p-values.
Alpha inflation
Alpha inflation occurs when multiple statistical tests increase the likelihood of Type I errors, compromising the interpretation of statistical significance; addressing this issue requires adjustments such as the Bonferroni correction to maintain the overall alpha level. Recognizing the distinction between statistical significance affected by alpha inflation and practical significance is critical for applying research findings meaningfully in scientific contexts.
Effect size metrics
Effect size metrics quantify the magnitude of relationships or differences in data, providing essential insight beyond p-values in statistical significance tests. Metrics such as Cohen's d, Pearson's r, and odds ratios enable researchers to assess practical significance by evaluating the real-world impact and relevance of findings.
Clinical significance
Statistical significance indicates the likelihood that a result is not due to chance, while clinical significance assesses the real-world impact of findings on patient outcomes, emphasizing measurable improvements in health or quality of life. Understanding clinical significance is essential in medical research to ensure that statistically significant results translate into meaningful benefits for patient care and treatment decisions.
Practical effect estimation
Practical effect estimation emphasizes the real-world impact of findings by quantifying the magnitude and relevance of effects beyond mere statistical significance, ensuring results translate into meaningful applications. This approach integrates confidence intervals and effect sizes to assess the tangible benefits and implications for decision-making in scientific research.
Minimal detectable effect (MDE)
The minimal detectable effect (MDE) quantifies the smallest true effect size that a statistical test can reliably identify, bridging the gap between statistical significance and practical relevance. Understanding MDE enables researchers to design studies with adequate power, ensuring that observed effects are not only statistically significant but also meaningful in real-world applications.
Fragility index
The Fragility Index quantifies the robustness of statistical significance by measuring how many event changes would alter study results from significant to non-significant, highlighting the difference between statistical and practical significance. Studies with a low Fragility Index often indicate results that may lack practical reliability despite achieving traditional p-value thresholds.
Statistical versus substantive significance
Statistical significance indicates the likelihood that a result is not due to chance, often represented by a p-value below a threshold such as 0.05, whereas practical significance assesses the real-world relevance or impact of the effect size observed in a study. Researchers must evaluate both statistical metrics and substantive significance to determine whether findings translate into meaningful changes or decisions beyond mere numerical evidence.
Real-world impact assessment
Statistical significance determines whether results are unlikely due to chance, often measured by p-values below a threshold like 0.05, but it does not indicate the magnitude or relevance of an effect. Practical significance assesses the real-world impact and usefulness of findings by considering effect size, cost-benefit analysis, and applicability to actual scenarios beyond mere statistical metrics.
Bayes factor threshold
Bayes factor thresholds offer a more nuanced measure of statistical evidence compared to traditional p-values by quantifying the strength of support for hypotheses, thus enhancing the assessment of both statistical and practical significance. A Bayes factor above 10 is typically considered strong evidence favoring the alternative hypothesis, underscoring the importance of interpreting results within the context of effect size and real-world relevance.
Statistical Significance vs Practical Significance Infographic
 industrydif.com
industrydif.com